01:35 Применение теории эволюции Дарвина в процессе оптимизации конструкций | |
Применение теории эволюции дарвина в процессе оптимизации конструкций В.А. Ходяков, В.Г. Пастушков  Вопрос оптимизации несущих конструкций сегодня актуален как никогда. Первостепенной задачей инженера является обеспечение требуемой несущей способности с минимальными затратами материала и труда на строительство и содержание. При этом существует бесконечное множество конструктивных решений с различными технико-экономическими показателями. Для оптимизации конструкций в пределах конкретной инженерной задачи предлагается использовать метод, в основе которого лежит теория эволюции Ч. Дарвина. Ключевые слова: эволюция, оптимизация, минимизация, арка, балка, ген, Grasshopper, Galapagos, Karamba. Для несложных задач с малым количеством параметров можно составлять несколько вариантов конструкций, анализируя и с каждым новым вариантом постепенно приближая их к наилучшим технико-экономические показателям (ТЭП). Для более сложных задач зачастую существует несколько вариантов оптимальных ТЭП, к которым мы можем прийти методом последовательного приближения. Но нахождение всех этих минимумов подбором – довольно сложная задача. Мебель своими руками создается тоже на основании наработок, опыта и размышлений современного человека о наилучших технико-экономических показателях конечного продукта. При использовании модели эволюции Дарвина мы не просто последовательно приближаем задачу оптимизации к решению, но и всегда оставляем шанс на обнаружение того, что данное направление приближения неверно и при принципиально другой комбинации параметров существует другое, лучшее решение – другой минимум ТЭП. На базе компьютерной программы Rhinoceros существует параметрический плагин Grasshopper, используя который можно довольно удобно механизировать процесс подбора вариантов несущей конструкции. В качестве плагина к Grasshopper существует программа Karamba, которая может анализировать конструкции с использованием метода конечных элементов. Karamba приходится очень кстати, когда требуется оптимизировать ТЭП несущей конструкции. Вся система моделирования и расчета в Grasshopper построена на использовании нодов (небольших элементарных функций) и построения между ними логических связей. Главной и наиболее интересной функцией является нод Galapagos, который и позволяет нам моделировать процесс дарвиновской эволюции. У нода существует два логических входа: Genome («Геном») и Fitness («Приспособленность»). Простым примером совместной работы Galapagos и Karamba является «эволюция» балки в арку. Балка пролетом 50 м оперта на две шарнирно неподвижные опоры и загружена распределенной нагрузкой 100 кН·м. В данном случае геномом являлись координаты контрольных точек по оси z, по которым строилась арка. В качестве приспособленности была заданна минимальная сумма модулей моментов в каждом из конечных элементов. В результате мы получили арку параболической формы, в которой эпюра моментов была практически сведена к нулю. В каждом поколении «рождается» некоторое количество особей (в данном случае 50). Каждая особь имеет свой набор генов или, как в данном случае, ген, в какойто степени отличающийся от генов предыдущего поколения. Если особь сильно отдаляется от условия приспособленности, то погибает и ген, носителем которого она является, погибает вместе с ней. В результате выживают наиболее приспособленные индивиды – точки. Важным является то, что если одна особь получила ген, сильно отличающийся от генов абсолютного большинства своих сородичей в лучшую сторону, то она начинает «переманивать» весь процесс эволюции на себя. Таким образом, в очень сложных задачах никогда нельзя быть уверенным, что эволюция пошла в правильном направлении. Всегда может найтись особь, которая «выпрыгнет» из общей массы и «перетянет» весь процесс на себя. Однако процесс оптимизации можно считать завершенным, когда несколько сот поколений не появляется следующая особь с лучшим геном. Таким образом, балка постепенно «приспособилась» к жизни с минимальными моментами, превратившись в арку. Было замечено, что моменты на разных участках арки существенно различаются (на вариантах с большей высотой арки это явление пропадает), после чего было добавлено еще одно условие приспособленности: минимальная разница между средним моментом по всем элементам и моментом в каждом элементе. После повторной оптимизации моменты по всей длине арки выровнялись и уменьшились до 50–60 кН·м. Использование законов эволюции Дарвина открывает большой простор для исследований. Были поставлены эксперименты по оптимизации несимметрично нагруженных арок, главным условием являлась также минимизация изгибающих моментов. Подбор оптимального сечения сборной двутавровой балки с минимальной затратой материалов является относительно сложной задачей. Была смоделирована система, условием приспособленности которой стала минимизация объема материала, при сохранении несущей способности, а в качестве генома, состоящего из четырех генов, выступали геометрические характеристики сечения двутавра: ширина и высота полок и стенки. В результате мы получили максимально экономичные, с точки зрения материалоемкости, сечения (рис. 1). Коэффициент использования сечения в центре пролета балки для напряжений от момента и для касательного напряжения у опор превышает 99,995 % во всех трех случаях. 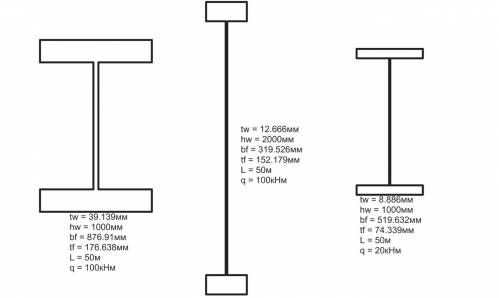 Проверка несущей способности производилась только по напряжениям от изгибающих моментов и касательных напряжений без учета коэффициентов. Сталь 10ХСНД, предел текучести 390 МПа. Список литературы 1. Хайман Э.В. Новая морфология архитектуры. Зачем гены зданиям? 2. Robert Stuart Smith. Видеолекция о формообразовании | |
|
| |
Обговорення Применение теории эволюции Дарвина в процессе оптимизации конструкций - 14 Травня 2014, коментарі та відгуки: | |